Visual Basic program "VB BHmerger" - Description and operation
Contents
Introduction and Purpose
The purpose of the Visual Basic program "BHmerger" is to demonstrate:
- That it is possible that photons can circulate around a blackhole
- What is involved if two Black Holes merge.
- The influence of a third BH.
To download an executable select: VB BHmerger.zip
This zip file contains 1 program:
- "VB BHmerger.exe" written in Visual Basic 5.0.
The same program is also available in VB2010. To download an executable select: VB2010 BHmerger.zip
This zip file contains 1 program:
- "VB2010 BHmerger.exe" written in Visual Basic 2010
For e description of that program select: Visual Basic program "VB2010 BHmerger" - Description and operation
For more information goto: Implementation details
2. Description
The Visual basic program program "VB BHmerger" consits of 2 Forms (or displays):
- Control Form. This form is used to Start the program and to modify the parameters.
- Display Form. This form shows the results of the simulation in a graphical form.
3. Operation - Control Form
Operation of the program is done from the Control Form.
The Controm Form uses 5 Commands: Start, Cont, Next,End and Stop. This depends about were you are during the simulation or program execution.
- The Start command is used to start the program. The purpose is to change the control parameters.
After selecting the Start command, the command changes into Cont.
- The Cont command is used to start the simulation.
After selecting the Cont command is removed.
- The Next command is used to finish the simulation.
The Display form shows the final result of the simulation.
After selecting the Next command, the command changes into Start in order to start the next simulation.
- The End command is used to terminate the program
- The Stop command is used to stop the simulation
 Picture 1A
Picture 1A
|
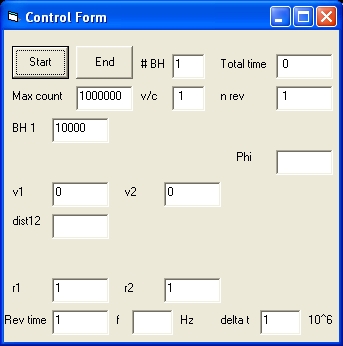
- Picture 1A shows the control display in case of one BH and a lightray.
The Control Form in case of 1 BH uses the following control paramaters:
- # BH , Max count , v/c , BH 1 , dist12 and freq
-
The parameter # BH defines the number of Black Holes.
- #BH = 1 : One Black hole and a "mass less" particle or photon.
- #BH = 2 : Two Black Holes.
- #BH = 3 : One binary Black Hole pair and a third smaller Black Hole.
In case of # BH = 1 the following control parameters are used:
- The parameter Max count defines the number of iterations in the first revolution.
- The parameter v/c defines the speed of the second object relative to the speed of light.
- The parameter BH 1 defines the mass of BH 1 in sun masses.
- The parameter dist12 defines the distance between object 1 and object 2.
With # BH = 1 the parameter dist12 defines the radius of the "mass less" particle.
With v/c = 1 the parameter dist12 defines the radius of a photon circling around a BH.
- The parameter freq is the number of revolutions per second.
|
The Control Display also shows the following parameters:
- v1 this is the speed of the BH and is equal to zero.
- v2 this is the speed of the light ray.
- r1 the distance of the BH from the center of gravity. In this case = 0
- r2 the distance of the lightray from the center of gravity. In this case = dist12
- Rev time is Revolution time. In the case: 2 * pi * r / v with r = dist12 and v = v2.
- f = frequency. In this case f = 1/"Rev time"
- delta t is step size. In this case "Rev time"/"Max counter"
3.1 Operation - Control Form. Parameter # BH = 1
In case # BH = 1 there are three ways to control the simulation.
-
Select BH 1 and v/c
In that case the parameters dist12 and freq are calculated
For Example:
- Select: "Start".
Enter first parameter # BH = 10000 and than enter parameter v/c = 1
Select "Cont"
-
The following table shows the result of 7 tests:
| Test | BH 1 | v/c | dist12 | f | total time |
| 1 | 10000 | 1 | 14766 | 3.23 | .3094 |
| 2 | 10000 | 0.5 | 59065 | 0.40 | 2.4758 |
| 3 | 10000 | 0.25 | 236261 | 0.05 | 19.8067 |
| 4 | 100000 | 1 | 147663 | 0.32 | 3.0948 |
| 5 | 1000 | 1 | 1476.6 | 32.31 | .0309 |
| 6 | 100 | 1 | 147.6 | 323.1 | .0031 |
| 7 | 36+29 | 1 | 95.9 | 497.1 | .0020 |
|
- In the tests 1-3 the mass of the BH is constant and the speed of the "mass less" particle varies.
What the results show is that how slower the speed how larger the radius = distance
- In the tests 4-7 the speed of the "mass less" particle is constant and the mass of the BH varies.
What the results show is that how smaller the mass how smaller the radius = distance
|
-
Select BH 1 and dist12
In that case the parameters v/c and freq are calculated
When the parameter v/c greater than one parameter v/c is set equal to 1 and the parameter
BH 1 is also calculated.
For Example:
- Select: "Start".
Enter first parameter # BH = 10000 and than enter parameter dist12 = 14766
Select "Cont"
-
The following table shows the result of 9 tests:
| Test | BH 1 | dist12 | v/c | f | total time |
| 1 | 10000 | 14766 | 1 | 3.231 | .3095 |
| 2 | 10000 | 20000 | .859 | 2.049 | .4878 |
| 3 | 10000 | 40000 | .607 | .724 | 1.3797 |
| 4 | 10000 | 80000 | .429 | .256 | 3.9026 |
| 5 | 10000 | 160000 | .303 | 0.090 | 11.0383 |
| 6 | 10000 | 320000 | .214 | 0.032 | 31.2211 |
| 7 | 6772 | 10000 | 1 | 4.771 | .2095 |
| 8 | 677 | 1000 | 1 | 47.71 | .0209 |
| 9 | 68 | 100 | 1 | 477.13 | .0021 |
|
- In all the tests the mass of the Black Hole initialy is 10000.
- Test 1 shows the situation when the "Mass less" particle is a photon.
- The test 2-6 show the situation when distance of the "Mass less" particle is larger than test 1
Between tests 2 and 4 the differance in distance is a factor 4, in v/c a factor 2 and in f a factor 8
The same between the tests "3 and 4" and "4 and 6".
- The test 7-9 show the situation when the "Mass less" particle is a photon and the distance is smaller than test 1
|
-
Select BH 1 and freq
In that case the parameters v/c and dist12 are calculated
When the parameter v/c greater than one parameter v/c is set equal to 1 and the parameter
BH 1 is also calculated.
For Example:
- Select: "Start".
Enter first parameter # BH = 10000 and than enter parameter f = 1
Select "Cont"
-
The following table shows the result of 4 tests:
| Test | BH 1 | f | v/c | dist12 | total time |
| 1 | 10000 | 3.23 | 1 | 14766 | .3095 |
| 2 | 10000 | 2 | .852 | 20331 | .5 |
| 3 | 10000 | 1 | .676 | 32274 | 1 |
| 4 | 10000 | 0.5 | .536 | 51231 | 2 |
| 5 | 6462 | 5 | 1 | 9542 | .2 |
| 6 | 4771 | 10 | 1 | 4771 | .1 |
| 7 | 2385 | 20 | 1 | 2385 | .05 |
|
- In all the tests the mass of the Black Hole initialy is 10000.
- Test 1 shows the situation when the "Mass less" particle is a photon.
- In the tests 2-4 the frequency f is less than the frequency of test 1
- In the tests 5-7 the frequency f is larger than the frequency of test 1
|
3.2 Operation - Control Form. Parameter # BH = 2
Picture 1B
|
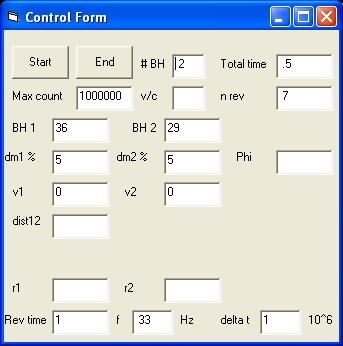
- Picture 1B shows the control display in case of two BH's
The Control Form in case of 1 BH uses the following control parameters:
# BH , Max count , v/c , BH 1 , BH 2 , dm1 % , dm2 % , dist12 and freq
In case # BH = 2 there are three ways to control the simulation.
- Enter the parameters: BH 1 , BH 2 and v/c
In that case the parameters: dist12 and freq are calculated.
- Enter the parameters: BH 1 , BH 2 and freq
In that case the parameters: dist12 and v/c are calculated.
- Enter the parameters: BH 1 , BH 2 and dist12
In that case the parameters: v/c and freq are calculated.
|
3.3 Operation - Control Form. Parameter # BH = 3
 Picture 1C
Picture 1C
|
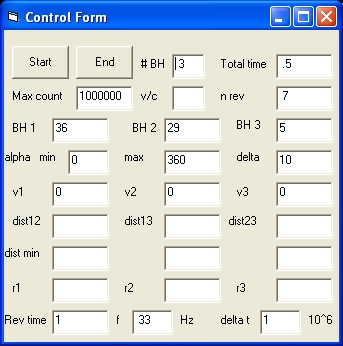
- Picture 1C shows the control display in case of three BH's
The Control Form in case of 1 BH uses the following control parameters:
# BH , Max count , v/c , BH 1 , BH 2 , BH 3 , dist12 and freq
alpha min, alpha max and delta
In case # BH = 3 there are also three ways to control the simulation as explained above.
- The parameter alpha min defines the minimum angle of alpha. The standard value is 0.
- The parameter alpha max defines the maximum angle of alpha. The standard value is 360.
- The parameter delta defines the delta angle of alpha. The standard value is 10.
- when you use the standard values and you select "Start" the simulation will perform 36 simulations with the angles: 0,10,20 etc until 360 degrees.
When alpha max = 0 you only will perform one simulation.
|
4. Display Form
The "Display Form" shows the result of the simulation.
Picture 2A
# BH = 1
|
Picture 2B
# BH = 2
|
Picture 2C
BH #3 = 5 m0
|
Picture 2D
BH #3 = 10 m0
|
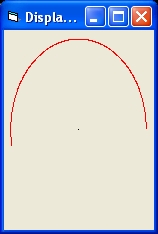
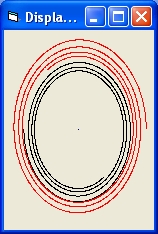
- Picture 2A shows the results of a simulation of 1 Black Hole and one light ray for one revolution.
The initial display shows roughly the half of the first revolution.
When the picture is selected you will observe the full revolution.
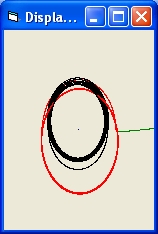
- Picture 2B shows the results of a simulation of 2 Black Holes for 7 revolutions.
The largest BH (object 1) is in black. The smallest BH (object 2) is in red.
The initial display shows roughly 3 revolutions.
When the picture is selected you will observe the full 7 revolutions.
- Picture 2C shows the results of a simulation of 3 Black Holes for two angles:
- alpha = 0 and alpha = 180 degrees
-
For the images of all angles between 0 and 360 degrees in increments of 10 degrees select Picture 2C. or select this link:
36 Merger Displays. BH = 5 m0 In this particular case mass of BH #3 = 5 solar masses
- Picture 2D shows the results of a simulation of 3 Black Holes for two angles:
- alpha = 0 and alpha = 180 degrees
-
For the images of all angles between 0 and 360 degrees in increments of 10 degrees select Picture 2D.or select this link:
36 Merger Displays. BH = 10 m0 In this particular case mass of BH #3 = 10 solar masses
4.1 Program Evaluation with two Black Holes.
The purpose of these test is to observe the behaviour of 2 BH's
Test 1 is the galibration test
| Test | BH 1 | BH 2 | dm1 % | dm2 % | v/c | n rev | dist12 | total time | freq | v1 | v2 |
| 1 | 36 | 29 | 0 | 0 | 0.224 | 10 | 586.7 | 0.3040 | 32.887 | 54095 | 67153 |
| 2 | 50.5 | 29 | 5 | 0 | 0.224 | 10 | 479.6 | 0.2452 | 48.464 | 54095 | 94227 |
| 3 | 36 | 41.1 | 0 | 5 | 0.224 | 10 | 494.6 | 0.2538 | 45.653 | 76674 | 67153 |
| 4 | 48.8 | 39.3 | 5 | 5 | 0.224 | 10 | 432.4 | 0.2172 | 59.347 | 73409 | 91129 |
| 5 | 31.9 | 25.7 | -1 | -1 | 0.224 | 10 | 660.8 | 0.3408 | 26.295 | 48032 | 59626 |
| 6 | 26.5 | 21.3 | -2 | -2 | 0.224 | 10 | 796.2 | 0.4000 | 18.724 | 39865 | 49487 |
- Test 1 shows the situation when the mass of the two Black Hole's are fixed. This shows a stable configuration.
- Test 2-4 show the situation where there is a positive influx of mass in a binary BH system: the two will spiral together.
- Test 5-6 show the situation where there is a negative influx of mass in a binary BH system: the two will spiral apart.
The positive influx can be simulated by introducing a third "large" object or a small BH.
In the second set of tests Test 1 is also a calibration test.
In this particular case the mass of the two BH's is identical
| Test | BH 1 | BH 2 | dm1 % | dm2 % | v/c | n rev | dist12 | total time | freq | v1 | v2 |
| 1 | 30 | 30 | 0 | 0 | 0.224 | 10 | 441.4 | 0.2065 | 48.422 | 67153 | 67153 |
| 2 | 42.3 | 30 | 5 | 0 | 0.224 | 10 | 366.3 | 0.1693 | 69.304 | 67153 | 94691 |
| 3 | 30 | 42.3 | 0 | 5 | 0.224 | 10 | 366.3 | 0.1693 | 69.304 | 94691 | 67153 |
| 4 | 40.7 | 40.7 | 5 | 5 | 0.224 | 10 | 325.3 | 0.1475 | 87.382 | 99129 | 91129 |
| 5 | 37.5 | 22.5 | 2.5 | -2.5 | 0.224 | 10 | 441.4 | 0.2065 | 48.422 | 50365 | 83941 |
| 6 | 45 | 14.9 | 5 | -5 | 0.224 | 10 | 441.4 | 0.2065 | 48.222 | 33576 | 100730 |
- Test 1 shows the situation when the mass of the two Black Hole's are fixed and identical. This shows a stable symetric configuration.
- Test 2-4 show the situation where there is a positive influx of mass in a binary BH system: the two will spiral together.
- Test 5-6 show the situation where the total mass in a binary BH system is constant: the distance between the two will stay constant (and = 60).
4.2 Program evaluation with two Black Holes and a third large object.
The following table shows the results for mass of BH #3 = 5 solar masses.
BH1 36 BH2 29 BH3 5 nrev 10 alpha min 0 max 360 delta 10 v1 54157 v2 67229 v3 0 Event GW 150914
alpha 0 nBH 2 m1 40.9 m2 29.0 nrev 10 r1 238 r2 338 r3 382 d12 448 d13 93 d23 668 ttime 0.301 f 34.9
alpha 10 nBH 2 m1 40.9 m2 29.0 nrev 10 r1 168 r2 239 r3 341 d12 371 d13 101 d23 648 ttime 0.241 f 44.5
alpha 20 nBH 2 m1 40.9 m2 29.0 nrev 10 r1 128 r2 181 r3 321 d12 298 d13 110 d23 607 ttime 0.205 f 53.1
alpha 30 nBH 2 m1 40.9 m2 29.0 nrev 10 r1 107 r2 151 r3 263 d12 255 d13 117 d23 555 ttime 0.188 f 58.5
alpha 40 nBH 2 m1 40.9 m2 29.0 nrev 10 r1 100 r2 142 r3 196 d12 240 d13 121 d23 510 ttime 0.184 f 59.8
alpha 50 nBH 2 m1 40.9 m2 29.0 nrev 10 r1 102 r2 145 r3 162 d12 246 d13 119 d23 484 ttime 0.191 f 57.0
alpha 60 nBH 2 m1 40.9 m2 29.0 nrev 10 r1 113 r2 160 r3 141 d12 271 d13 113 d23 463 ttime 0.209 f 51.2
alpha 70 nBH 2 m1 40.9 m2 29.0 nrev 10 r1 133 r2 188 r3 125 d12 308 d13 105 d23 438 ttime 0.243 f 42.8
alpha 80 nBH 2 m1 40.9 m2 29.0 nrev 10 r1 179 r2 253 r3 192 d12 360 d13 94 d23 407 ttime 0.324 f 31.0
alpha 90 nBH 2 m1 36.0 m2 33.9 nrev 1 r1 297 r2 314 r3 312 d12 518 d13 84 d23 57 ttime 0.500 f 32.5
alpha 100 nBH 2 m1 36.0 m2 33.9 nrev 3 r1 1707 r2 1808 r3 278 d12 511 d13 89 d23 60 ttime 0.500 f 5.2
alpha 110 nBH 2 m1 36.0 m2 33.9 nrev 10 r1 335 r2 355 r3 261 d12 500 d13 106 d23 70 ttime 0.487 f 20.0
alpha 120 nBH 2 m1 36.0 m2 33.9 nrev 4 r1 2845 r2 3013 r3 605 d12 327 d13 127 d23 35 ttime 0.500 f 20.9
alpha 130 nBH 2 m1 36.0 m2 33.9 nrev 4 r1 739 r2 784 r3 309 d12 452 d13 76 d23 57 ttime 0.500 f 12.1
alpha 140 nBH 2 m1 40.9 m2 29.0 nrev 10 r1 51 r2 73 r3 344 d12 102 d13 98 d23 89 ttime 0.252 f 43.9
alpha 150 nBH 2 m1 36.0 m2 33.9 nrev 2 r1 1736 r2 1838 r3 315 d12 529 d13 548 d23 60 ttime 0.500 f 4.9
alpha 160 nBH 2 m1 36.0 m2 33.9 nrev 5 r1 820 r2 868 r3 378 d12 522 d13 607 d23 63 ttime 0.500 f 11.0
alpha 170 nBH 2 m1 36.0 m2 33.9 nrev 9 r1 547 r2 580 r3 419 d12 496 d13 643 d23 68 ttime 0.500 f 19.5
alpha 180 nBH 2 m1 36.0 m2 33.9 nrev 10 r1 294 r2 311 r3 452 d12 439 d13 654 d23 75 ttime 0.329 f 31.7
alpha 190 nBH 2 m1 36.0 m2 33.9 nrev 10 r1 174 r2 184 r3 414 d12 328 d13 629 d23 86 ttime 0.231 f 46.7
alpha 200 nBH 2 m1 36.0 m2 33.9 nrev 10 r1 110 r2 116 r3 297 d12 223 d13 557 d23 101 ttime 0.181 f 61.6
alpha 210 nBH 2 m1 40.9 m2 29.0 nrev 10 r1 46 r2 65 r3 373 d12 104 d13 102 d23 127 ttime 0.225 f 48.6
alpha 220 nBH 2 m1 40.9 m2 29.0 nrev 10 r1 154 r2 219 r3 489 d12 322 d13 80 d23 152 ttime 0.481 f 20.3
alpha 230 nBH 2 m1 40.9 m2 29.0 nrev 3 r1 1330 r2 1881 r3 412 d12 444 d13 70 d23 169 ttime 0.500 f 5.6
alpha 240 nBH 2 m1 40.9 m2 29.0 nrev 2 r1 496 r2 703 r3 350 d12 454 d13 70 d23 181 ttime 0.500 f 4.0
alpha 250 nBH 2 m1 40.9 m2 29.0 nrev 4 r1 358 r2 505 r3 292 d12 459 d13 72 d23 191 ttime 0.500 f 6.5
alpha 260 nBH 2 m1 40.9 m2 29.0 nrev 6 r1 324 r2 459 r3 228 d12 459 d13 78 d23 205 ttime 0.500 f 12.7
alpha 270 nBH 3 m1 36.0 m2 29.0 nrev 10 r1 305 r2 379 r3 7103 d12 239 d13 117 d23 232 ttime 0.229 f 44.7
alpha 280 nBH 2 m1 40.9 m2 29.0 nrev 7 r1 888 r2 1255 r3 289 d12 317 d13 74 d23 275 ttime 0.500 f 9.1
alpha 290 nBH 2 m1 39.2 m2 29.0 nrev 10 r1 291 r2 394 r3 238 d12 180 d13 113 d23 336 ttime 0.251 f 52.4
alpha 300 nBH 2 m1 39.0 m2 29.0 nrev 10 r1 164 r2 221 r3 263 d12 147 d13 110 d23 292 ttime 0.255 f 49.5
alpha 310 nBH 2 m1 36.0 m2 33.9 nrev 10 r1 119 r2 126 r3 399 d12 128 d13 83 d23 76 ttime 0.286 f 34.8
alpha 320 nBH 2 m1 40.9 m2 29.0 nrev 6 r1 571 r2 807 r3 294 d12 531 d13 78 d23 545 ttime 0.500 f 12.1
alpha 330 nBH 2 m1 40.9 m2 29.0 nrev 7 r1 390 r2 552 r3 288 d12 531 d13 79 d23 599 ttime 0.500 f 15.1
alpha 340 nBH 2 m1 40.9 m2 29.0 nrev 9 r1 396 r2 560 r3 375 d12 517 d13 82 d23 639 ttime 0.500 f 19.3
alpha 350 nBH 2 m1 40.9 m2 29.0 nrev 10 r1 335 r2 474 r3 397 d12 493 d13 86 d23 664 ttime 0.394 f 26.0
alpha 360 nBH 2 m1 40.9 m2 29.0 nrev 10 r1 234 r2 333 r3 399 d12 448 d13 93 d23 668 ttime 0.301 f 34.9
- The parameter d12 shows the nearest distance between object 1 and 2.
The closest distance are simulated with alpha = 140 and alpha= 210.
- The parameter f shows the frequency between object 1 and object 2.
The higest frequency are simulated with alpha = 40 and alpha= 290.
The following table shows the results for mass of BH #3 = 10 solar masses.
BH1 36 BH2 29 BH3 10 nrev 10 alpha min 0 max 360 delta 10 v1 54157 v2 67229 v3 0
alpha 0 nBH 2 m1 45.9 m2 29.0 nrev 10 r1 245 r2 390 r3 395 d12 372 d13 84 d23 655 ttime 0.406 f 26.2
alpha 10 nBH 2 m1 45.9 m2 29.0 nrev 10 r1 125 r2 201 r3 326 d12 261 d13 91 d23 647 ttime 0.232 f 48.9
alpha 20 nBH 2 m1 45.9 m2 29.0 nrev 10 r1 74 r2 120 r3 299 d12 163 d13 99 d23 618 ttime 0.169 f 70.5
alpha 30 nBH 2 m1 44.6 m2 29.0 nrev 10 r1 48 r2 76 r3 312 d12 109 d13 105 d23 579 ttime 0.145 f 81.6
alpha 40 nBH 2 m1 44.1 m2 29.0 nrev 10 r1 50 r2 77 r3 221 d12 86 d13 107 d23 543 ttime 0.139 f 84.6
alpha 50 nBH 2 m1 44.7 m2 29.0 nrev 10 r1 45 r2 71 r3 188 d12 85 d13 105 d23 521 ttime 0.147 f 78.8
alpha 60 nBH 2 m1 36.0 m2 38.9 nrev 1 r1 33238 r2 30682 r3 410 d12 460 d13 95 d23 49 ttime 0.500 f 35.8
alpha 70 nBH 2 m1 36.0 m2 38.9 nrev 1 r1 30746 r2 28382 r3 382 d12 472 d13 93 d23 51 ttime 0.500 f 34.9
alpha 80 nBH 2 m1 36.0 m2 38.9 nrev 1 r1 28772 r2 26560 r3 351 d12 480 d13 87 d23 52 ttime 0.500 f 33.8
alpha 90 nBH 2 m1 36.0 m2 38.9 nrev 1 r1 27311 r2 25210 r3 327 d12 480 d13 80 d23 53 ttime 0.500 f 32.4
alpha 100 nBH 2 m1 36.0 m2 38.9 nrev 1 r1 25123 r2 23192 r3 303 d12 474 d13 74 d23 55 ttime 0.500 f 31.2
alpha 110 nBH 2 m1 36.0 m2 38.9 nrev 1 r1 18274 r2 16870 r3 272 d12 460 d13 72 d23 58 ttime 0.500 f 32.0
alpha 120 nBH 3 m1 36.0 m2 29.0 nrev 10 r1 136 r2 169 r311725 d12 97 d13 81 d23 87 ttime 0.154 f 71.6
alpha 130 nBH 2 m1 36.0 m2 38.9 nrev 3 r1 980 r2 906 r3 121 d12 140 d13 112 d23 74 ttime 0.500 f 4.4
alpha 140 nBH 2 m1 44.5 m2 29.0 nrev 10 r1 281 r2 433 r3 170 d12 242 d13 105 d23 137 ttime 0.392 f 45.6
alpha 150 nBH 1 m1 37.5 m2 29.0 nrev 1 r1 19 r2 28 r3 282 d12 48 d13 89 d23 62 ttime 0.048 f 44.8
alpha 160 nBH 2 m1 36.0 m2 38.9 nrev 0 r1 23161 r2 21379 r3 358 d12 552 d13 563 d23 56 ttime 0.500 f 32.9
alpha 170 nBH 2 m1 36.0 m2 38.9 nrev 0 r1 10439 r2 9636 r3 395 d12 552 d13 617 d23 60 ttime 0.500 f 32.9
alpha 180 nBH 2 m1 36.0 m2 38.9 nrev 7 r1 785 r2 725 r3 440 d12 371 d13 642 d23 67 ttime 0.500 f 15.6
alpha 190 nBH 2 m1 36.0 m2 38.9 nrev 10 r1 131 r2 121 r3 437 d12 218 d13 632 d23 76 ttime 0.236 f 48.1
alpha 200 nBH 2 m1 36.0 m2 37.5 nrev 10 r1 47 r2 44 r3 353 d12 85 d13 580 d23 87 ttime 0.144 f 82.5
alpha 200 nBH 2 m1 36.0 m2 38.9 nrev 15 r1 53 r2 47 r3 342 d12 82 d13 581 d23 87 ttime 0.203 f 86.2
alpha 210 nBH 1 m1 45.9 m2 29.0 nrev 1 r1 33 r2 53 r3 555 d12 86 d13 74 d23 112 ttime 0.210 f 45.3
alpha 220 nBH 2 m1 45.9 m2 29.0 nrev 1 r1 18056 r2 28639 r3 492 d12 311 d13 64 d23 137 ttime 0.500 f 43.5
alpha 230 nBH 2 m1 45.9 m2 29.0 nrev 1 r1 22159 r2 35149 r3 457 d12 339 d13 62 d23 155 ttime 0.500 f 41.7
alpha 240 nBH 2 m1 45.9 m2 29.0 nrev 1 r1 20910 r2 33165 r3 362 d12 360 d13 63 d23 166 ttime 0.500 f 39.8
alpha 250 nBH 2 m1 45.9 m2 29.0 nrev 1 r1 16756 r2 26579 r3 298 d12 373 d13 67 d23 171 ttime 0.500 f 38.5
alpha 260 nBH 2 m1 45.9 m2 29.0 nrev 1 r1 5745 r2 9113 r3 246 d12 381 d13 74 d23 174 ttime 0.500 f 37.7
alpha 270 nBH 3 m1 36.0 m2 29.0 nrev 10 r1 326 r2 404 r3 3906 d12 102 d13 104 d23 177 ttime 0.193 f 54.4
alpha 280 nBH 2 m1 36.0 m2 33.8 nrev 10 r1 345 r2 367 r3 246 d12 122 d13 152 d23 77 ttime 0.221 f 42.3
alpha 290 nBH 2 m1 36.0 m2 37.7 nrev 10 r1 317 r2 302 r3 200 d12 118 d13 237 d23 103 ttime 0.201 f 63.8
alpha 300 nBH 2 m1 45.9 m2 29.0 nrev 2 r1 17950 r2 28470 r3 308 d12 361 d13 66 d23 236 ttime 0.500 f 14.8
alpha 310 nBH 2 m1 44.6 m2 29.0 nrev 10 r1 122 r2 190 r3 320 d12 262 d13 98 d23 227 ttime 0.220 f 63.6
alpha 320 nBH 2 m1 36.0 m2 36.6 nrev 10 r1 249 r2 244 r3 125 d12 154 d13 73 d23 74 ttime 0.171 f 77.8
alpha 330 nBH 2 m1 45.9 m2 29.0 nrev 0 r1 11461 r2 18179 r3 308 d12 555 d13 72 d23 544 ttime 0.500 f 32.9
alpha 340 nBH 2 m1 45.9 m2 29.0 nrev 0 r1 5001 r2 7934 r3 313 d12 553 d13 74 d23 601 ttime 0.500 f 32.9
alpha 350 nBH 2 m1 45.9 m2 29.0 nrev 4 r1 832 r2 1320 r3 377 d12 441 d13 78 d23 639 ttime 0.500 f 9.2
alpha 360 nBH 2 m1 45.9 m2 29.0 nrev 10 r1 245 r2 390 r3 390 d12 372 d13 84 d23 655 ttime 0.406 f 26.2
- The parameter r1 and r2 show the final distance of the objects #1 and #2.
In 10 cases the distance is roughly 5000 or more, which implies that as a result of the merging of object #3 with either object #1 or object #2, both are ejected.
This is the case with alpha: 60,70,80,90,100,110,160,170,220,230,240,250,260,300, 330 and 340.
- The shortest distance between object #1 and #2 d12 is at alpha 150 = 48.
- The higest frequence is at alpha 40 = 84.6
5. Simulation of BH merger

Picture 3
|
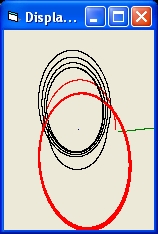
- Picture 3 shows a simulation of a BH merger of 2 BH's and a third object of 12 solar masses
Object 3 first merges with BH #1. This is the largest BH. After this the object evaporates. The merging start when the third object reaches a speed above the speed of light.
This is the largest BH and then two BH's spiral together.
- When Picture 3 is selected you will see the Control form at the end of the simulation.
It is the smallest BH #2 that will reach the final speed of 300000 km/sec. That means the smallest BH in a sense that collides with the largest BH.
- What you can also see from the Control Form that the rotation frequency of the two BH's, which started at 33 HZ at the end was 88 HZ.
- In order to perform the simulation the following parameters are selected:
# BH = 3, BH 1 = 36, BH 2 = 29, BH 3 = 12.
nREv = 10. This values should at least be larger than 7 other wise the simulation stops to early.
alpha min = 40 or 50 alpha max = 0. Zero indicates 1 simulation.
f = 33 Hz
|
6. Reflection
The merging of the BH's or objects in the simulation is "controlled" by the speed of light. Generally speaking by the concept that an object can not move faster than the speed of light. If an object reaches that speed than it will physical desintegrate. In reality this desintegration can already start slower an at a much lower speed. This means that the whole process of desintegration will happen smoother.
Of course you can ask yourself the question what has the speed of light to do with the physical behaviour of Black Holes? Generally speaking nothing. It has also nothing to do with the broader concept of radiation. All the limiting physical factors are inherent (internally) in the structure of the Black Holes.
You can also raise the question if the behaviour has anything to do with Newton''s Law or General Relativity? IMO neither Newton's Law nor General Relativity have anything to do with the behaviour or evolution of physical objects.
The only thing that you can say that similar processes are described by the same mathematics or laws. As such if you observe something different (or new) you know that a different (or new) physical process is at stake which require new or modified mathematics.
7. Feedback
-
"LIGO. What happened 1.3 billion years ago."
https://groups.google.com/forum/?fromgroups#!topic/sci.astro.research/hdlp6rSyiYc
In this discussion I raise the the supposition that maybe a third object is involved.
In posting # 2 Phillip Helbig replies:
- Due to energy loss via gravitational waves, the orbits decayed until they merged.
-
The first issue is how much energy loss is there in a single BH of 100 solar masses compared to a binary BH system of 100 solar masses each. IMO there is no difference.
This is based on the concept that at a large distance of an object it is possible based on the revolution time and the distance to calculate the mass of the central object, but not if the central object in reality is a binary system. To do that you have to measure or calculate the distance (fluctuations) very accurate.
In most cases this is very difficult.
The advantage of LIGO is that the fluctuations were measured directly. However not in distance but in the strength of the gravitational field which directly influenced the LIGO apparatus.
When you consider a comet around the Sun there is energy/mass transfer between the comet and the Sun. In such a "binary" system the total mass will be constant.
When the two collide this will have a consequence for the Earth which distance towards the Sun will slightly decrease.
You can only speak of energy loss in a binary BH system when one of the BH (#1) will explode and become a supernova (Or when the sun becomes a red giant). The loss of energy or mass is not detected instantaneously but only when the ejected material reaches the orbit of second BH. After that moment the circumference of the second BH will increase and finally follow a straight line.
- "Did LIGO Detect Dark Matter? - New paper on arxiv.org"
https://groups.google.com/forum/?fromgroups#!topic/sci.astro.research/Rbdjx0o38Ek
In message #17 of 30 March 2016 the following document is discussed:
http://arxiv.org/abs/1602.02444
"Binary Black Hole Mergers from Globular Clusters: Masses, Merger Rates,
and the Impact of Stellar Evolution"
This document is interesting because the starting point is the behaviour of Globular Clusters which are considered the birth place of (neutron) stars and small Black Holes. What the document does not discuss (?) is what is the cause that an ordinary star of roughly 30 sollar masses changes into a Black Hole.
At page 2 of the document we read:
- The merger time is then the sum of the inspiral time and the time at which the binary is ejected from the cluster.
-
This is part of the problem of the article: the emphasis is on ejection from the cluster. What we are looking for is what is happening inside the cluster.
At page 5 of the document we read:
- A hard binary (with binding energy greater than the typical kinetic energy of particles in the cluster), typically undergoes a series of strong encounters with other single and binary stars.
-
This is a strong indication for: collisions between single stars and a binary BH.
Created 1 March 2016
Updated 9 March 2016
Back to my home page: Contents of This Document







